Bộ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động - Phần 8

30/08/2021
25 Câu hỏi
582 Lượt xem

Trắc Nghiệm Hay giới thiệu đến các bạn Bộ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động - Phần 8. Tài liệu bao gồm 25 câu hỏi kèm đáp án thuộc danh mục Khoa học - Kỹ thuật. Tài liệu này sẽ giúp các bạn ôn tập, củng cố lại kiến thức để chuẩn bị cho các kỳ thi sắp tới. Mời các bạn tham khảo!

3.5 8 Đánh giá

Thi Ngay

Cập nhật ngày

18/10/2021

Thời gian

30 Phút

Tham gia thi

52 Lần thi

Câu 1: Hệ thống bất biến theo thời gian là hệ thống có:

A. Tín hiệu ra không thay đổi theo thời gian

B. Phương trình vi phân mô tả hệ thống không thay đổi

C. Tín hiệu vào không thay đổi theo thời gian

D. Hệ số của phương trình vi phân mô tả hệ thống không thay đổi

Câu 2: Tìm nghiệm của hệ thống có phương trình đặc tính sau: s2+ 4s + 3 = 0

A. s1= -0.268; s2= -3.732

B. s1= -0.586; s2= -3.414

C. s1= -1; s2= -3

D. s1= -2; s2= -2

Câu 3: Hệ thống có quỹ đạo nghiệm số như hình vẽ. Số nghiệm cực của hệ thống là:

A. 2

B. 3

C. 4

D. 5

Câu 4: Biểu đồ Bode biên độ của khâu tích phân lý tưởng G(s)=1/s

A. đi qua điểm ω =0 và có độ dốc là 20dB/dec

B. đi qua điểm ω =0 và có độ dốc là -20dB/dec

C. đi qua điểm ω =1 và có độ dốc là 20dB/dec

D. đi qua điểm ω =1và có độ dốc là -20dB/dec

Câu 5: Hệ SISO là hệ thống có:

A. Nhiều ngõ vào- nhiều ngõ ra

B. Nhiều ngõ vào - một ngõ ra

C. Một ngõ vào – một ngõ ra

D. Một ngõ vào – nhiều ngõ ra

Câu 6: Số lần đổi dấu của số hạng ở cột 1 bảng Routh bằng số nghiệm:

A. Có phần thực âm

B. Có phần thực dương

C. Nghiệm phức của phương trình

D. Có phần thực bằng 0

Câu 7: Hàm truyền đạt của hệ thống nối tiếp:

A. G(s)= Tổng của các Gi(s)

B. G(s) = Tích của các Gi(s)

C. G(s)= Hiệu của các Gi(s)

D. Tỉ số giữa tín hiệu ra và tín hiệu vào

Câu 8: DAC là:

A. Bộ chuyển đổi tín hiệu từ dạng số sang dạng tương tự

B. Bộ khuếch đại tín hiệu

C. Bộ chuyển đổi tín hiệu từ dạng tương tự sang dạng số

D. Bộ thay đổi tần số của tín hiệu vào

Câu 9: Hàm truyền của hệ thống:

A. Là tỉ số giữa tín hiệu ra và tín hiệu vào

B. Là tỉ số giữa biến đổi Laplace của tín hiệu ra và biến đổi Laplace của tín hiệu vào khi điều kiện đầu bằng 0

C. Phụ thuộc vào tín hiệu ra và tín hiệu vào

D. Mô tả chức năng của các phần tử và sự tác động qua lại giữa chúng trong hệ

Câu 10: Hệ thống rời rạc là ổn định nếu tất cả các nghiệm của phương trình đặc tính:

A. Nằm bên trái mặt phẳng phức

B. Nằm bên trong vòng tròn đơn vị

C. Nằm bên ngoài vòng tròn đơn vị

D. Nằm bên phải mặt phẳng phức

Câu 11: Hàm truyền đạt \(G(s) = \frac{{{V_o}(s)}}{{{V_i}(s)}}{\cos ^{ - 1}}\theta \) của mạch điện ở hình sau là: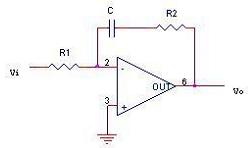

A. \(- \frac{{{R_2}}}{{{R_1}}} - \frac{1}{{{R_1}Cs}}\)

B. \(- \frac{{{R_2}}}{{{R_1}}} + \frac{1}{{{R_1}Cs}}\)

C. \(\frac{{{R_2}}}{{{R_1}}} + \frac{1}{{{R_1}Cs}}\)

D. \( - \frac{{{R_1}}}{{{R_2}}} - \frac{1}{{{R_1}Cs}}\)

Câu 12: Đặc điểm của khâu hiệu chỉnh PD (Proportional Derivative) là:

A. Làm chậm đáp ứng của hệ thống, tăng thời gian quá độ

B. Làm chậm đáp ứng của hệ thống, giảm thời gian quá độ

C. Làm nhanh đáp ứng của hệ thống, giảm thời gian quá độ

D. Làm nhanh đáp ứng của hệ thống, tăng thời gian quá độ

Câu 13: Tiêu chuẩn IAE (Integral of the Absolute magnitude of the Error - tích phân trị tuyệt đối biên độ sai số ):

A. \({J_1} = \int\limits_{ - \infty }^{ + \infty } {|e(t)|dt}\)

B. \({J_1} = \int\limits_0^{ + 1} {|e(t)|dt} \)

C. \({J_1} = \int\limits_0^{ + \infty } {|e(t)|dt}\)

D. \({J_1} = \int\limits_{ - \infty }^{ + \infty } {|e(t)|dt} \)

Câu 14: Cho hệ thống hồi tiếp âm đơn vị sau. Sai số xác lập exl là: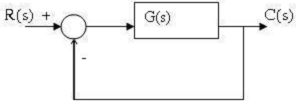

A. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)}}\)

B. \({e_{xl}} = \mathop {\lim }\limits_{t \to 0} e(t) = \mathop {\lim }\limits_{s \to \infty } \frac{{sR(s)}}{{1 + G(s)}}\)

C. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{R(s)}}{{1 + G(s)}}\)

D. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sG(s)}}{{1 + R(s)}}\)

Câu 15: Cho hệ thống hồi tiếp âm đơn vị sau. Sai số xác lập exl là: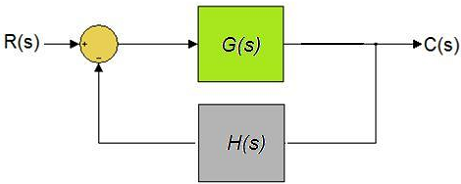

A. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)H(s)}}\)

B. \({e_{xl}} = \mathop {\lim }\limits_{t \to 0} e(t) = \mathop {\lim }\limits_{s \to \infty } \frac{{sR(s)}}{{1 + G(s)H(s)}}\)

C. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{R(s)}}{{1 + G(s)}}\)

D. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sG(s)}}{{1 + R(s)G(s)}}\)

Câu 16: Xác định hàm truyền tương đương của hệ thống nối tiếp như hình vẽ: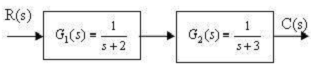

A. \({G_{td}}(s) = \frac{1}{{{s^2} + 5s + 2}}\)

B. \({G_{td}}(s) = \frac{{s + 2}}{{{s^2} + 5s + 6}}\)

C. \({G_{td}}(s) = \frac{1}{{{s^2} + 3s + 6}}\)

D. \({G_{td}}(s) = \frac{1}{{{s^2} + 5s + 6}}\)

Câu 17: Hàm truyền tương đương của hệ thống hồi tiếp như hình vẽ là: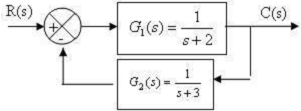

A. \({G_{td}}(s) = \frac{{s + 3}}{{{s^2} + 5s + 7}}\)

B. \({G_{td}}(s) = \frac{{s + 2}}{{{s^2} + 5s + 7}}\)

C. \({G_{td}}(s) = \frac{1}{{{s^2} + 5s + 2}}\)

D. \({G_{td}}(s) = \frac{{s + 2}}{{{s^2} + 5s + 6}}\)

Câu 18: Cho hệ thống có cấu trúc sau:

A. \({G_{td}}(s) = \frac{{3s + 10}}{{5{s^3} + 16{s^2} + 11s + 10}}\)

B. \({G_{td}}(s) = \frac{{3s + 9}}{{5{s^3} + 16{s^2} + 11s + 11}}\)

C. \({G_{td}}(s) = \frac{{3s + 9}}{{5{s^3} + 16{s^2} + 11s + 10}}\)

D. \({G_{td}}(s) = \frac{{s + 9}}{{5{s^3} + 16{s^2} + 11s + 10}}\)