Câu hỏi:
Hệ thống có quỹ đạo nghiệm số như hình vẽ. Số nghiệm cực của hệ thống là: 616d40577a588.png)
A. 2
B. 3
C. 4
D. 5
Câu 1: Cho hệ thống có hàm truyền tương đương sau: ![]()
A. Hệ thống không ổn định, có 3 nghiệm cực bên phải mặt phẳng phức
B. Hệ thống ổn định, có 2 nghiệm cực nằm bên trái mặt phẳng phức
C. Hệ thống không ổn định, có 2 nghiệm cực bên phải mặt phẳng phức, 1 nghiệm cực bên trái mặt phẳng phức
D. Hệ thống ở biên giới ổn định, có 1 nghiệm cực nằm trên trục ảo, 2 nghiệm cực bên trái mặt phẳng phức
30/08/2021 4 Lượt xem
Câu 2: Cho hàm truyền \(G(s) = \frac{2}{{{s^2} + 2s + 8}}\) , hãy lập phương trình trạng thái
A. \(A = \left[ {\begin{array}{*{20}{c}} 0&1\\ { - 8}&{ - 2} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 2 \end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\)
B. \(A = \left[ {\begin{array}{*{20}{c}} 0&1\\ { - 2}&{ - 1} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 20 \end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\)
C. \(A = \left[ {\begin{array}{*{20}{c}} 0&1\\ { - 8}&{ - 2} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 20 \end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\)
D. \(A = \left[ {\begin{array}{*{20}{c}} 1&1\\ { - 2}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 20\\ 0 \end{array} \right]{\rm{ ; C = }}\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]\)
30/08/2021 3 Lượt xem
Câu 3: Cho hệ thống hồi tiếp âm đơn vị sau. Sai số xác lập exl là: 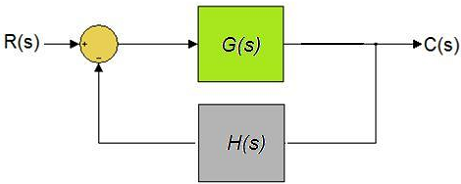
A. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sR(s)}}{{1 + G(s)H(s)}}\)
B. \({e_{xl}} = \mathop {\lim }\limits_{t \to 0} e(t) = \mathop {\lim }\limits_{s \to \infty } \frac{{sR(s)}}{{1 + G(s)H(s)}}\)
C. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{R(s)}}{{1 + G(s)}}\)
D. \({e_{xl}} = \mathop {\lim }\limits_{t \to \infty } e(t) = \mathop {\lim }\limits_{s \to 0} \frac{{sG(s)}}{{1 + R(s)G(s)}}\)
30/08/2021 3 Lượt xem
Câu 4: Hàm truyền đạt của hệ thống nối tiếp:
A. G(s)= Tổng của các Gi(s)
B. G(s) = Tích của các Gi(s)
C. G(s)= Hiệu của các Gi(s)
D. Tỉ số giữa tín hiệu ra và tín hiệu vào
30/08/2021 3 Lượt xem
Câu 5: Hàm truyền đạt \(G(s) = \frac{{{V_o}(s)}}{{{V_i}(s)}}{\cos ^{ - 1}}\theta \) của mạch điện ở hình sau là: 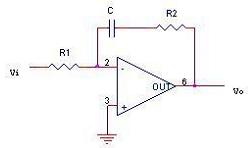
A. \(- \frac{{{R_2}}}{{{R_1}}} - \frac{1}{{{R_1}Cs}}\)
B. \(- \frac{{{R_2}}}{{{R_1}}} + \frac{1}{{{R_1}Cs}}\)
C. \(\frac{{{R_2}}}{{{R_1}}} + \frac{1}{{{R_1}Cs}}\)
D. \( - \frac{{{R_1}}}{{{R_2}}} - \frac{1}{{{R_1}Cs}}\)
30/08/2021 3 Lượt xem
Câu 6: Đặc điểm của khâu hiệu chỉnh PD (Proportional Derivative) là:
A. Làm chậm đáp ứng của hệ thống, tăng thời gian quá độ
B. Làm chậm đáp ứng của hệ thống, giảm thời gian quá độ
C. Làm nhanh đáp ứng của hệ thống, giảm thời gian quá độ
D. Làm nhanh đáp ứng của hệ thống, tăng thời gian quá độ
30/08/2021 3 Lượt xem

Câu hỏi trong đề: Bộ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động - Phần 8
- 58 Lượt thi
- 30 Phút
- 25 Câu hỏi
- Sinh viên
Cùng chủ đề Bộ câu hỏi trắc nghiệm Lý thuyết điều khiển tự động có đáp án
- 1.9K
- 144
- 25
-
64 người đang thi
- 1.8K
- 163
- 20
-
23 người đang thi
- 1.6K
- 113
- 25
-
29 người đang thi
- 1.0K
- 77
- 25
-
39 người đang thi




Chia sẻ:
Đăng Nhập để viết bình luận