
250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
- 30/11/2021
- 30 Câu hỏi
- 466 Lượt xem
Trắc Nghiệm Hay giới thiệu đến các bạn 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1). Tài liệu bao gồm 30 câu hỏi kèm đáp án thuộc danh mục Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số. Tài liệu này sẽ giúp các bạn ôn tập, củng cố lại kiến thức để chuẩn bị cho các kỳ thi sắp tới. Mời các bạn tham khảo!
Cập nhật ngày
30/11/2021
Thời gian
30 Phút
Tham gia thi
1 Lần thi
Câu 1: Hàm số nào sau đây đồng biến trên tập số thực R?
A. y = x4 – 2x2 – 5
B. y = - x + 1
C. C. ![]()
D. y = x3 + 3x – 1
Câu 2: Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
(I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
A. A. I và II
B. Chỉ I
C. C. I và III
D. D. II và III
Câu 3: Cho hàm số
(m khác 1)
Chọn câu trả lời đúng
A. A. Hàm số luôn giảm trên (-∞;1) và (1;+∞) với m < 1
B. B. Hàm số luôn giảm trên tập xác định.
C. C. Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1
D. D. Hàm số luôn tăng trên (-∞;1) và (1;+∞)
Câu 5: Hàm số nào sau đây nghịch biến trên R.
A. A. y = -x3 + 2x2 – x – 1
B. B. y = 1/3 x3 – x2 + 3x + 1
C. C. y = -1/3.x3 + x2 – x.
D. D. y = -x3 + 3x + 1
Câu 7: Hàm số nào sau đây nghịch biến trên R?
A. A. y = -x3 + 3x2 + 3x – 2.
B. B. y = -x3 + 3x2 – 3x – 2
C. C. y = x3 + 3x2 + 3x – 2
D. D. y = x3 – 3x2 – 3x – 2
Câu 8: Hàm số nào sau đây nghịch biến trên R?
A. A. y = -x3 + 3x2 + 3x – 2
B. B. y = -x3 + 3x2 – 3x – 2.
C. C. y = x3 + 3x2 + 3x – 2
D. D. y = x3 – 3x2 – 3x – 2.
Câu 10: Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (-1;1)?
A. A. y = 1/x
B. B. y = x3 – 3x + 1
C. C. y = 1/x2
D. D. y = -1/x
Câu 11: Cho hàm số f(x) = -2x3 + 3x2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?
A. A. Hàm số nghịch biến trên R
B. B. f(a) > f(b).
C. C. f(b) < 0
D. D. f(a) < f(b).
Câu 12: Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
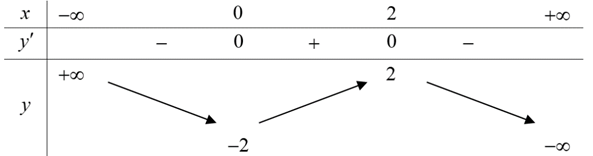

A. A. y = x3 – 3x2 – 1
B. B. y = -x3 + 3x2 – 2
C. C. y = -x3 + 3x2 – 1
D. D. y = -x3 – 3x – 2
Câu 13: Cho hàm số y = f(x) = x3 + 3x. Hỏi khẳng định nào sau đây là khẳng định đúng?
A. A. Hàm số f(x) đồng biến trên R
B. B. Hàm số f(x) nghịch biến trên (-1;0)
C. C. Hàm số f(x) nghịch biến trên (-∞;0).
D. D. Hàm số f(x) không đổi trên R
Câu 14: Đâu là hàm số đồng biến trên đoạn [2;5]?
A. A. y = x
B. B. y = x(x+1)(x+2)
C. C. y = x(x+1)(x+2)(x+3)(x+4)
D. D. Cả A, B và C đều đúng
Câu 16: Tìm tất cả các giá trị thực của tham số m đề hàm số nghịch biến trên khoảng (1;+∞)
A. A. 0 < m ≤ 1
B. B. 0 < m < 1
C. C. m > 1
D. D. 0 ≤ m < 1
Câu 17: Với giá trị nào của m thì hàm số đồng biến trên khoảng (1;+∞)
A. A.
B. B.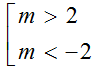
C. C.m>2
D. D.m<-2
Câu 19: Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là đường thẳng
A. A. song song với đường thẳng x = 1
B. B. song song với trục hoành
C. C. có hệ số góc dương.
D. D. có hệ số góc bằng -1
Câu 20: Đồ thị của hàm số y = x4 – x2 + 1 có bao nhiêu điểm cực trị có tung độ dương?
A. A. 1
B. B. 2.
C. C. 3.
D. D. 4
Câu 21: Khẳng định nào sau đây là khẳng định sai về hàm số
A. A. Hàm số đồng biến trên (1; +∞)
B. B. Hàm số đồng biến trên từng khoảng xác định.
C. C. Hàm số có cực trị
D. D. Hàm số đồng biến trên (-∞;-1)
Câu 22: Cho hàm số y = 2x3 + 3x2 – 12x - 12. Gọi x1, x2 lần lượt là hoành độ hai điểm cực đại và cực tiểu của đồ thị hàm số. Kết luận nào sau đây là đúng?
A. A. (x1 – x2)2 = 8
B. B. x1x2 = 2
C. C. x2 – x1 = 3
D. D. x12 + x22 = 6
Câu 23: Hỏi hàm số y = x3 – 3x2 – 9x – 2 đạt cực tiểu tại điểm nào?
A. A. x = -3
B. B. x = -1
C. C. x = 1
D. D. x = 3
Câu 24: Tìm tất cả các điểm cực đại của hàm số y = -x4 + 2x2 + 1
A. A. x = ±1
B. B. x = -1
C. C. x = 1
D. D. x = 0
Câu 25: Hàm số nào dưới đây không có cực trị?
A. A. y = x4 + x2
B. B. y = x2 - 1
C. C. y = x3 – x2
D. D. y = x3 + 3x
Câu 28: Gọi x1, x2 là hai điểm cực trị của hàm số Tính giá trị của biểu thức P = x1.x2
A. A. P = -5
B. B. P = -2
C. C. P = -1
D. D. P = -4
Câu 29: Cho hàm số tìm khẳng định đúng?
A. A. Hàm số đã cho có đạt cực tiểu duy nhất là y = 1
B. B. Hàm số đã cho đạt cực đại duy nhất là y = -1/2
C. C. Hàm số đã cho chỉ có giá trị cực tiểu là y = -1/2
D. D. Hàm số đã cho không có cực trị
Câu 30: Cho hàm số y = f(x) có đạo hàm trong khoảng (a, b) chứa điểm x0 (có thể trừ điểm x0). Tìm mệnh đề đúng trong các mệnh đề sau:
A. A. Nếu f(x) không có đạo hàm tại x0 thì f(x) không đạt cực trị tại x0
B. B. Nếu f’(x0) = 0 thì f(x) đạt cực trị tại điểm x0
C. C. Nếu f’(x0) = 0 và f’’(x0) = 0 thì f(x) không đạt cực trị tại điểm x0
D. D. Nếu f’(x0) = 0 và f’’(x0) ≠ 0 thì f(x) đạt cực trị tại điểm x0
Cùng danh mục Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- 361
- 1
- 24
-
94 người đang thi
- 368
- 2
- 20
-
28 người đang thi
- 575
- 8
- 20
-
18 người đang thi
- 433
- 0
- 20
-
39 người đang thi
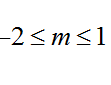
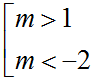
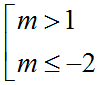
Chia sẻ:
Đăng Nhập để viết bình luận