Câu hỏi:
Trong các hàm số sau, hàm số nào luôn đồng biến trên từng khoảng xác định của nó?
(I) ; y = -x4 + x2 – 2 (II); y = x3 – 3x – 5 (III).
A. A. I và II
B. Chỉ I
C. C. I và III
D. D. II và III
Câu 1: Hàm số nào dưới đây không có cực trị?
A. A. y = x4 + x2
B. B. y = x2 - 1
C. C. y = x3 – x2
D. D. y = x3 + 3x
30/11/2021 0 Lượt xem
Câu 2: Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?
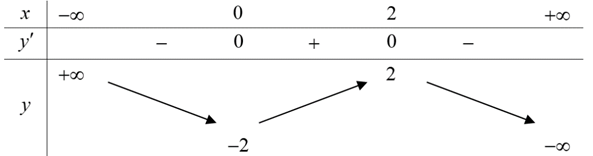

A. A. y = x3 – 3x2 – 1
B. B. y = -x3 + 3x2 – 2
C. C. y = -x3 + 3x2 – 1
D. D. y = -x3 – 3x – 2
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem
Câu 4: Cho hàm số f(x) = -2x3 + 3x2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?
A. A. Hàm số nghịch biến trên R
B. B. f(a) > f(b).
C. C. f(b) < 0
D. D. f(a) < f(b).
30/11/2021 0 Lượt xem
Câu 5: Cho hàm số
(m khác 1)
Chọn câu trả lời đúng
A. A. Hàm số luôn giảm trên (-∞;1) và (1;+∞) với m < 1
B. B. Hàm số luôn giảm trên tập xác định.
C. C. Hàm số luôn tăng trên (-∞;1) và (1;+∞) với m > 1
D. D. Hàm số luôn tăng trên (-∞;1) và (1;+∞)
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem

Câu hỏi trong đề: 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
- 1 Lượt thi
- 30 Phút
- 30 Câu hỏi
- Học sinh
Cùng danh mục Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- 363
- 1
- 24
-
44 người đang thi
- 369
- 2
- 20
-
36 người đang thi
- 576
- 8
- 20
-
43 người đang thi
- 435
- 0
- 20
-
55 người đang thi
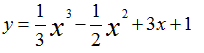
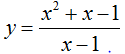
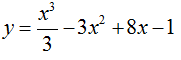
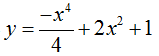
Chia sẻ:
Đăng Nhập để viết bình luận