Câu hỏi:
Gọi x1, x2 là hai điểm cực trị của hàm số Tính giá trị của biểu thức P = x1.x2
A. A. P = -5
B. B. P = -2
C. C. P = -1
D. D. P = -4
Câu 1: Trong các hàm số sau, hàm số nào nghịch biến trên các khoảng xác định của chúng
A. A.![]()
B. 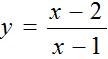
C. 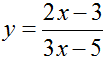
D. D.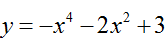
30/11/2021 0 Lượt xem
Câu 2: Đâu là hàm số đồng biến trên đoạn [2;5]?
A. A. y = x
B. B. y = x(x+1)(x+2)
C. C. y = x(x+1)(x+2)(x+3)(x+4)
D. D. Cả A, B và C đều đúng
30/11/2021 0 Lượt xem
Câu 3: Khẳng định nào sau đây là khẳng định sai về hàm số
A. A. Hàm số đồng biến trên (1; +∞)
B. B. Hàm số đồng biến trên từng khoảng xác định.
C. C. Hàm số có cực trị
D. D. Hàm số đồng biến trên (-∞;-1)
30/11/2021 0 Lượt xem
Câu 4: Hàm số nào dưới đây không có cực trị?
A. A. y = x4 + x2
B. B. y = x2 - 1
C. C. y = x3 – x2
D. D. y = x3 + 3x
30/11/2021 0 Lượt xem
Câu 5: Hỏi hàm số y = x3 – 3x2 – 9x – 2 đạt cực tiểu tại điểm nào?
A. A. x = -3
B. B. x = -1
C. C. x = 1
D. D. x = 3
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem

Câu hỏi trong đề: 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
- 1 Lượt thi
- 30 Phút
- 30 Câu hỏi
- Học sinh
Cùng danh mục Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- 363
- 1
- 24
-
70 người đang thi
- 369
- 2
- 20
-
98 người đang thi
- 576
- 8
- 20
-
56 người đang thi
- 435
- 0
- 20
-
21 người đang thi
Chia sẻ:
Đăng Nhập để viết bình luận