
200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao (P1)
- 30/11/2021
- 25 Câu hỏi
- 431 Lượt xem
Trắc Nghiệm Hay giới thiệu đến các bạn 200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao (P1). Tài liệu bao gồm 25 câu hỏi kèm đáp án thuộc danh mục Chương 3: Phương pháp tọa độ trong không gian. Tài liệu này sẽ giúp các bạn ôn tập, củng cố lại kiến thức để chuẩn bị cho các kỳ thi sắp tới. Mời các bạn tham khảo!
Cập nhật ngày
30/11/2021
Thời gian
25 Phút
Tham gia thi
0 Lần thi
Câu 1: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6x + 3y - 2z - 6 = 0
B. x + 2y + 3z - 14 = 0
C. x + 3y + 2z - 11 = 0
D.
Câu 3: Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C (0;0;c), trong đó a > 0, b > 0, c > 0. Mặt phẳng (ABC) đi qua điểm I (1;2;3) sao cho thể tích khối tứ diện OABC đạt giá trị lớn nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
A. a + b + c = 12
B. a2 + b = c - 6
C. a + b + c = 18
D. a + b - c = 0
Câu 4: Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
A. A. arccos(4/15)
B. 1
C. arcsin(4/5)
D. arccos(4/5)
Câu 5: Trong không gian Oxyz, cho điểm H (2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A, B, C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
A. 2x + y + z - 6 = 0
B. x + 2y + z - 6 = 0
C. x + 2y + 2z - 6 = 0
D. 2x + y + z + 6 = 0
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho các điểm A (0; 0; -2), B(4; 0; 0). Mặt cầu (S) có bán kính nhỏ nhất, đi qua O, A, B có tâm là:
A. A. I (0;0;-1)
B. I (2;0;0)
C. I (2;0;-1)
D. I (4/3;0;-2/3)
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho A (-3;0;0), B (0;0;3), C (0;-3;0) và mặt phẳng (P): x + y + z - 3 = 0. Tìm trên (P) điểm M sao cho nhỏ nhất.
A. A. M (3;3;-3)
B. M (-3;-3;3)
C. M (3;-3;3)
D. M (-3;3;3)
Câu 8: Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. A. 2x + y - 3z + 3 = 0
B. x + 2y - z - 1 = 0
C. 3x + 2y - z + 1 = 0
D. 2x - y - 3z + 3 = 0
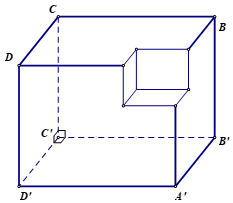
Câu 10: Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
A. A. 4a/3
B. a/3
C. 2a/3
D. 3a/4
Câu 11: Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
A. M (0;1;-4)
B. M (2;1;0)
C. M (0;1;-2)
D. M (0;1;4)
Câu 22: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5) và D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?
A. Có vô số mặt phẳng.
B. 1 mặt phẳng.
C. 7 mặt phẳng.
D. 4 mặt phẳng.
Câu 25: Trong không gian Oxyz, cho điểm A(1;0;-1), mặt phẳng (P): x + y - z - 3 = 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + √2. Phương trình mặt cầu (S) là:
A. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
B. (x - 2)2 + (y - 2)2 + (z - 1)2 = 9 và x2 + y2 + (z + 3)2 = 9
C. (x + 2)2 + (y - 2)2 + (z + 1)2 = 9 và (x + 1)2 + (y - 2)2 + (z + 2)2 = 9
D. (x + 1)2 + (y - 2)2 + (z + 2)2 = 9 và (x - 2)2 + (y - 2)2 + (z - 1)2 = 9
Cùng danh mục Chương 3: Phương pháp tọa độ trong không gian
- 433
- 0
- 25
-
60 người đang thi
- 388
- 1
- 15
-
74 người đang thi
- 398
- 2
- 15
-
51 người đang thi
- 353
- 2
- 15
-
34 người đang thi
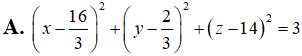
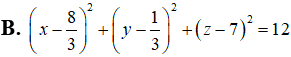
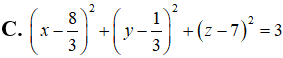
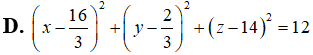
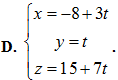
Chia sẻ:
Đăng Nhập để viết bình luận