Câu hỏi:
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Lấy điểm M thuộc đoạn AD', điểm N thuộc đoạn BD sao cho AM = DN = x, (0 < x < a√2/2). Tìm x theo a để đoạn MN ngắn nhất.
A.
B.
C.
D.
Câu 1: Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A'D.
A. A. 4a/3
B. a/3
C. 2a/3
D. 3a/4
30/11/2021 0 Lượt xem
Câu 2: Trong không gian với hệ tọa độ Oxyz cho điểm A (3;2;-1) và đường thẳng
Viết phương trình mặt phẳng (P) chứa d sao cho khoảng cách từ A đến (P) là lớn nhất.
A. A. 2x + y - 3z + 3 = 0
B. x + 2y - z - 1 = 0
C. 3x + 2y - z + 1 = 0
D. 2x - y - 3z + 3 = 0
30/11/2021 0 Lượt xem
Câu 3: Trong không gian với hệ tọa độ Oxyz, cho điểm M(1; 2; 3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
A. 1372/9
B. B. 686/9
C. C. 524/3
D. 343/9
30/11/2021 0 Lượt xem
Câu 4: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là: .
Cho ba điểm A, M, B nằm trên mặt cầu (S) sao cho góc AMB = . Diện tích tam giác AMB có giá trị lớn nhất bằng?
A. A. 4
B. 2
C. C. 4π
D. Không tồn tại.
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem
Câu 6: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(0;0;-6), B(0;1;-8), C(1;2;-5) và D(4;3;8). Hỏi có tất cả bao nhiêu mặt phẳng cách đều bốn điểm đó?
A. Có vô số mặt phẳng.
B. 1 mặt phẳng.
C. 7 mặt phẳng.
D. 4 mặt phẳng.
30/11/2021 0 Lượt xem

Câu hỏi trong đề: 200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao (P1)
- 0 Lượt thi
- 25 Phút
- 25 Câu hỏi
- Học sinh
Cùng danh mục Chương 3: Phương pháp tọa độ trong không gian
- 433
- 0
- 25
-
58 người đang thi
- 388
- 1
- 15
-
54 người đang thi
- 398
- 2
- 15
-
48 người đang thi
- 353
- 2
- 15
-
73 người đang thi
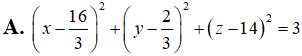
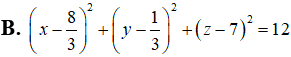
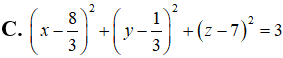
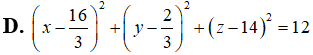
Chia sẻ:
Đăng Nhập để viết bình luận