Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(2;1;3), B(1;-1;2), C(3;-6;1). Điểm M(x;y;z) thuộc mặt phẳng (Oyz) sao cho MA2 + MB2 + MC2 đạt giá trị nhỏ nhất. Tính giá trị của biểu thức P = x+y+z
A. A. P = 0
B. P = 2P = 0
C. P = 6
D. P = -2
30/11/2021 0 Lượt xem
Câu 2: Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
A. A. arccos(4/15)
B. 1
C. arcsin(4/5)
D. arccos(4/5)
30/11/2021 0 Lượt xem
Câu 3: Trong không gian với hệ trục tọa độ Oxyz, cho bốn điểm A(2;-3;7), B(0;4;1), C(3;0;5) và D(3;3;3). Gọi M là điểm nằm trên mặt phẳng (Oyz) sao cho biểu thức đạt giá trị nhỏ nhất. Khi đó tọa độ của M là:
A. M (0;1;-4)
B. M (2;1;0)
C. M (0;1;-2)
D. M (0;1;4)
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem
Câu 5: Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình là: .
Cho ba điểm A, M, B nằm trên mặt cầu (S) sao cho góc AMB = . Diện tích tam giác AMB có giá trị lớn nhất bằng?
A. A. 4
B. 2
C. C. 4π
D. Không tồn tại.
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem

Câu hỏi trong đề: 200 câu trắc nghiệm Phương pháp tọa độ trong không gian nâng cao (P1)
- 0 Lượt thi
- 25 Phút
- 25 Câu hỏi
- Học sinh
Cùng danh mục Chương 3: Phương pháp tọa độ trong không gian
- 433
- 0
- 25
-
34 người đang thi
- 388
- 1
- 15
-
67 người đang thi
- 398
- 2
- 15
-
30 người đang thi
- 353
- 2
- 15
-
64 người đang thi
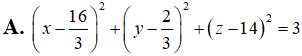
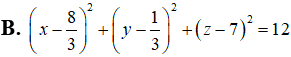
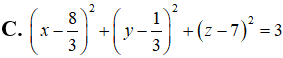
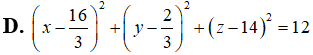
Chia sẻ:
Đăng Nhập để viết bình luận