Câu hỏi: Điện tích Q < 0 phân bố đều trên vòng dây tròn, tâm O, bán kính R. Chọn gốc điện thế ở vô cùng. Xét điện trường trên trục của vòng dây, phát biểu nào sau đây là đúng?

A. Tại tâm vòng dây, cường độ điện trường có giá trị lớn nhất và điện thế có giá trị nhỏ nhất. 

B. Tại tâm vòng dây, cường độ điện trường triệt tiêu và điện thế có giá trị lớn nhất.

C. Tại tâm vòng dây, cường độ điện trường triệt tiêu và điện thế có giá trị nhỏ nhất.

D. Tại tâm vòng dây, cường độ điện trường và điện thế đều triệt tiêu. 

Câu 1: Có hai điện tích điểm q1 = +2.10–6 C; q2 = –10–6 C cách nhau 10 cm. Giữ cố định q1. Khi q2 di chuyển ra xa thêm 90 cm dọc theo đường thẳng nối chúng thì công của lực điện trường là bao nhiêu?

A. +0,162 J.

B. –0,162 J.

C. +0,324 J.

D. –1,62 J.

Câu 2: Điện tích điểm Q < 0 ở tâm chung của hai đường tròn bán kính r và R (hình 4.6). Một hạt alpha (α) di chuyển trong điện trường của điện tích Q theo các quĩ đạo khác nhau. Phát biểu nào sau đây là đúng khi nói về công A của lực điện trường?

A. Nếu α đi từ A theo vòng tròn lớn đến D rồi đến C thì công có giá trị dương. 

B. Nếu α đi từ B theo vòng nhỏ lớn đến C thì công có giá trị âm. 

C. Nếu α đi từ C đến D rồi theo vòng tròn lớn đến A thì công có giá trị dương. 

D. Nếu α đi từ D theo vòng tròn lớn đến A rồi đến B thì công bằng không. 

Câu 3: Điện tích Q phân bố đều với mật độ điện khối ρ trong khối cầu tâm O, bán kính R, đặt trong không khí. Chọn gốc điện thế ở vô cùng. Biểu thức tính điện thế tại điểm M cách tâm O một khoảng r > R là: 

A. \({V_M} = \frac{{kQ}}{{2r}}\)

B. \({V_M} = \frac{{kQ}}{{r^2}}\)

C. \({V_M} = \frac{{\sigma {R^3}}}{{3{\varepsilon _0}r}}\)

D. \({V_M} = \frac{{4{R^3}}}{{3{\varepsilon _0}r}}\)

Câu 4: Đặt phân tử có mômen lưỡng cực pe = 6,24.10–30 Cm vào điện trường đều E = 3.104 V/m, sao cho \(\overrightarrow {{p_e}}\) hợp với \(\overrightarrow {{E}}\) một góc 300. Tính độ lớn của mômen ngẫu lực tác dụng lên phân tử.

A. 9,36.10–26 N.

B. 16,2. 10–26 Nm.

C. 16,2. 10–26 N.

D. 9,36.10–26 Nm. 

Câu 5: Điện tích điểm +Q ở tâm đường tròn như hình 4.7. So sánh công A1 và A2 của lực điện trường khi điện tích điểm q < 0 đi theo đường gấp khúc BAC và theo cung BC.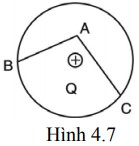

A. A1 > A2

B. A1 < A2. 

C. A1 = A2

D. A1 = A2 = 0. 

Câu 6: Dây thẳng, rất dài, tích điện đều, mật độ điện dài λ < 0, đặt trong không khí. Biết biểu thức tính cường độ điện trường tại điểm M cách dây một đoạn x là \(E = \frac{{2k\left| \lambda \right|}}{x}\) . Chọn gốc điện thế tại điểm M0 cách dây một đoạn x0 = 1 mét. Tìm biểu thức tính điện thế tại điểm M. 

A. VM = +2k|λ|lnx. 

B. VM = +2k|λ|.x.

C. VM = –2k|λ|lnx. 

D. VM = - 2k|λ|.x.