Câu hỏi: Hàm truyền của hiệu chỉnh tỉ lệ P (proportional) liên tục có dạng:

A. \({G_C}(s) = {K_p} + {K_D}s\)

B. \({G_C}(s) = {K_p}s + {K_D}\)

C. \({G_C}(s) = {K_p} + \frac{{{K_D}}}{s}\)

D. \({G_C}(s) = {K_p}\)

Câu 1: Hàm truyền của hiệu chỉnh vi phân tỉ lệ PD (proportional derivative) liên tục có dạng:

A. \({G_C}(s) = {K_p} + {K_D}\)

B. \({G_C}(s) = {K_p} + {K_D}s\)

C. \({G_C}(s) = {K_p}s + {K_D}\)

D. \({G_C}(s) = {K_p} + \frac{{{K_D}}}{s}\)

Câu 2: Các trạng thái cân bằng gồm:

A. Biên giới ổn định, ổn định

B. Ổn định, không ổn định

C. Biên giới ổn định, ổn định, không ổn định

D. Biên giới ổn định, không ổn định

Câu 3: Cho phương trình 2s4+s3+3s2+5s+10=0  .Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm có phần  thực dương:

A. Hệ thống ổn định, có 4 nghiệm nằm bên trái mặt phẳng phức

B. Hệ thống không ổn định, có 3 nghiệm bên phải mặt phẳng phức, 1 nghiệm bên trái mặt phẳng phức

C. Hệ thống không ổn định, có 2 nghiệm bên phải mặt phẳng phức, 2 nghiệm bên trái mặt phẳng phức

D. Hệ thống không ổn định, có 1 nghiệm bên phải mặt phẳng phức, 3 nghiệm bên trái mặt phẳng phức

Câu 4: Cho hệ có phương trình đặc trưng. Xét tính ổn định của hệ thống, và cho biết có bao nhiêu nghiệm có phần thực dương:

A. Hệ thống không ổn định, có 2 nghiệm có phần thực dương 

B. Hệ thống không ổn định, có 3 nghiệm có phần thực dương 

C. Hệ thống không ổn định, có 1 nghiệm có phần thực dương 

D. Hệ thống ổn định, có 4 nghiệm nằm bên trái mặt phẳng phức

Câu 5: Cho hàm truyền \(G(s) = \frac{5}{{{s^3} + 8{s^2} + 9s + 2}}\)    hãy lập phương trình trạng thái:

A. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ { - 2}&{ - 9}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 5 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)

B. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ 2&9&8 \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 5 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)

C. \(A = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ { - 2}&{ - 9}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 0\\ 2 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 1 0}}} \right];\)

D. \(A = \left[ {\begin{array}{*{20}{c}} 1&1&0\\ 0&0&1\\ { - 2}&{ - 9}&{ - 8} \end{array}} \right]{\rm{ ; B = }}\left[ \begin{array}{l} 0\\ 1\\ 2 \end{array} \right]{\rm{ ; C = }}\left[ {1{\rm{ 0 0}}} \right];\)

Câu 6: Cho hệ thống có phương trình đặc trưng: 2s4 +s3 + 3s2 + 2s + 2 = 0 . Bảng Routh của hệ thống được cho như sau: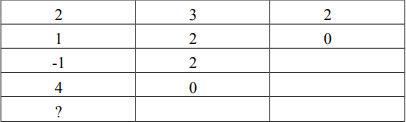

A. 2

B. 3

C. 4

D. 5