Câu hỏi:
Cho hàm số có đạo hàm . Hỏi hàm số có mấy điểm cực trị?
A. A. 2
B. B. 3
C. C. 4
D. D. 5
Câu 1: Cho hàm số . Khẳng định nào sau đây là đúng?
A. A. Hàm số có ba điểm cực trị
B. B. Hàm số chỉ có đúng 2 điểm cực trị
C. C. Hàm số không có cực trị
D. D. Hàm số chỉ có đúng một điểm cực trị
30/11/2021 0 Lượt xem
Câu 2: Hàm số bậc ba có thể có bao nhiêu điểm cực trị?
A. A. 0 hoặc 1 hoặc 2
B. B. 1 hoặc 2
C. C. 0 hoặc 2
D. D. 0 hoặc 1
30/11/2021 0 Lượt xem
Câu 3: Cho hàm số . Khẳng định nào sau đây là đúng?
A. A. Hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 0
B. B. Hàm số đạt cực tiểu tại x = 2 và đạt cực đại x = 0.
C. C. Hàm số đạt cực đại tại x = -2 và cực tiểu tại x = 0.
D. D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = -2
30/11/2021 0 Lượt xem
Câu 4: Cho hàm số có đồ thị như hình vẽ
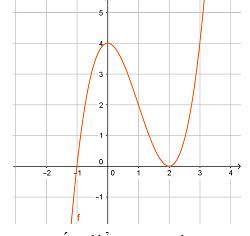
Đồ thị hàm số có mấy điểm cực trị?

A. A. 2
B. B. 1.
C. C. 0
D. D. 3
30/11/2021 0 Lượt xem
Câu 5: Cho hàm số xác định trên và thuộc đoạn . Khẳng định nào sau đây là khẳng định đúng?
A. A. Hàm số đạt cực trị tại thì hoặc
B. B. Hàm số đạt cực trị tại thì
C. C.Hàm số đạt cực trị tại thì nó không có đạo hàm tại
D. D. Nếu hàm số đạt cực trị tại thì hàm số không có đạo hàm tại hoặc
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem

Câu hỏi trong đề: Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1)
- 1 Lượt thi
- 50 Phút
- 30 Câu hỏi
- Học sinh
Cùng danh mục Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- 469
- 1
- 30
-
82 người đang thi
- 363
- 1
- 24
-
60 người đang thi
- 369
- 2
- 20
-
97 người đang thi
- 576
- 8
- 20
-
98 người đang thi
Chia sẻ:
Đăng Nhập để viết bình luận