Câu hỏi:

Giả sử y = f(x) có đạo hàm cấp hai trên (a;b). Nếu $\left\{\begin{array}{c}f\text{'}\left(x_0\right)=0\\ f\text{'}\text{'}\left(x_0\right)>0\end{array}\right.$ thì:

Cho hàm số y = f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng (a;b) và $x_0\in \left(a,b\right)$. Khẳng định nào sau đây là sai?

Cho hàm số y = f(x) có bảng biến thiên như sau:

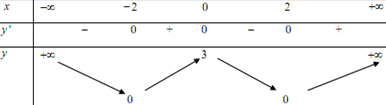
Khẳng định nào sau đây là khẳng định sai:

Cho hàm số y = f(x) có đạo hàm trên (a;b). Nếu f'(x) đổi dấu từ dương sang âm qua điểm $x_0$ thì:

Chọn phát biểu đúng:

Nếu $x_0$ là điểm cực đại của hàm số thì $\left(x_0;f\left(x_0\right)\right)$ là:

Cho hàm số $y=f\left(x\right)$ có đạo hàm trên (a;b). Nếu $f\text{'}\left(x\right)$ đổi dấu từ âm sang dương qua điểm $x_0$ thuộc (a;b) thì: