Câu hỏi:

Cho hai đường thẳng d và d’ song song có bao nhiêu phép tịnh tiến biến đường thẳng d thành đường thẳng d’:

A. Không có phép tịnh tiến nào.

B. Có duy nhất một phép tịnh tiến.

C. Có 2 phép tịnh tiến.

D. Có vô số phép tịnh tiến.

Câu 1:

Mệnh đề nào sau đây sai?                  

A. Thực hiện liên tiếp 2 phép dời hình ta được 1 phép dời hình

B. Phép vị tự là phép đồng dạng

C. Thực hiện liên tiếp 2 phép dời hình ta được 1 phép đồng dạng

D. Thực hiện liên tiếp 2 phép đồng dạng ta được 1 phép dời hình

Câu 2:

Cho A, B cố định. Phép biến hình F biến điểm M bất kì thành M’ sao cho $3\overrightarrow{MM\text{'}}=-2\overrightarrow{BA}$

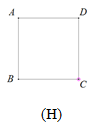
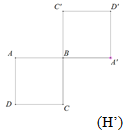
A. F là phép vị tựtâm A tỉ số -$\frac{2}{3}$

B. F là phép tịnh tiến theo vectơ $-\frac{2}{3}\overrightarrow{AB}$

C. F là phép vị tự tâm B tỉ số -$\frac{2}{3}$

D. F là phép tịnh tiến theo vectơ $\frac{-2}{3}\overrightarrow{BA}$

Câu 3:

Chọn phát biểu đúng:

A. Phép vị tự là phép dời hình

B. Phép quay là một phép dời hình

C. Phép dời hình là phép tịnh tiến

D. Phép biến hình là phép đối xứng trục

Câu 4:

Cho A, B cố định, hệ thức $\overrightarrow{MM\text{'}}+\overrightarrow{MB}=\overrightarrow{MA}$ cho ta M’ là ảnh của M qua:

A. Phép tịnh tiến $\overrightarrow{MA}$

B. Phép tịnh tiến $\overrightarrow{BA}$

C. Phép tịnh tiến $\overrightarrow{0}$

D. Phép tịnh tiến $\overrightarrow{AB}$

Câu 5:

Cho $A\text{'}=T_{\overrightarrow{u}}\left(A\right);B\text{'}=T_{\overrightarrow{u}}\left(B\right);C\text{'}=T_{\overrightarrow{u}}\left(C\right);D\text{'}=T_{\overrightarrow{u}}\left(D\right)$ và AB = BC + CD thì: 

A. A'B' = B'C' – C'D'     

B. A'C' = A'B' + D'C’  

C. B'C' = B'A' + A'C'  

D. A'B' = B'C' + C'D'

Câu 6:

Số phát biểuđúng:

1. Phép tịnh tiến biến đường thẳng thành đường thẳng song song với nó

2. Phép biến hình biến mỗiđiểm M thành chính nó dọi là phép đồng nhất

3. Phép đối xứng trục, phép quay, phép tịnh tiến đều bảo toàn khoảng cách giữa hai điểm

4. Phép đối xứng tâm biến đường thẳng thành đường thẳng song song với nó

5. Phép vị tự là một phép đồng dạng

6. Phép biến hình F’ có được nhờ thực hiện liên tiếp các phép tịnh tiến, phép quay, phép vị tự là phép đồng dạng

7. Phép biến hình F’ có được nhờ thực hiện liên tiếp các phép tịnh tiến, phép quay, phép vị tự là phép dời hình

A. 4

B. 5

C. 6

D. 7