Câu hỏi:

Biết rằng hàm số y = a${\mathrm{x}}^2$ + bx + c (a $\ne$ 0) đạt giá trị nhỏ nhất bằng 4 tại x = 2 và có đồ thị hàm số đi qua điểm A (0; 6). Tính tích P = abc.

A. P = -6

B. P = 6

C. P = -3

D. P = 32

Câu 1:

Xác định Parabol (P): y = a${\mathrm{x}}^2$ + bx + 2 biết rằng Parabol đi qua hai điểm M (1; 5) và N (2; −2).

A. y = −5${\mathrm{x}}^2$ + 8x + 2

B. y = 10${\mathrm{x}}^2$ + 13x + 2   

C. y = −10${\mathrm{x}}^2$ − 13x + 2    

D. y = 9${\mathrm{x}}^2$ + 6x – 5

Câu 2:

Tìm điểm A cố định mà họ đồ thị hàm số y = ${\mathrm{x}}^2$ + (2 − m)x + 3m( ${\mathrm{P}}_{\mathrm{m}}$) luôn đi qua.

A. A (3; 15)

B. A (0; −2)

C. A (3; −15)

D. A (−3; −15)

Câu 3:

Tìm tất cả các giá trị thực của m để phương trình −2${\mathrm{x}}^2$− 4x + 3 = m có nghiệm.

A. 1 ≤ m ≤ 5.

B. −4 ≤ m ≤ 0.

C. 0 ≤ m ≤ 4.

D. m ≤ 5.

Câu 4:

Tìm các giá trị của tham số m để phương trình $2x^2-2x+1-m=0$ có hai nghiệm phân biệt

A. $m>\frac{1}{2}$

B. Không tồn tại

Câu 5:

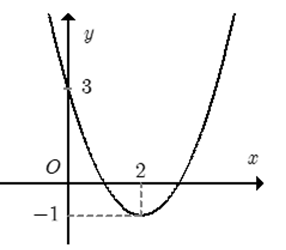
Tìm các giá trị thực của tham số m để phương trình |${\mathrm{x}}^2$ − 3x + 2| = m có bốn nghiệm thực phân biệt.

A. m $\ge \frac{1}{4}$

B. 0 < m < $\frac{1}{4}$

C. m = 0

D. Không tồn tại

Câu 6:

Tìm parabol (P): y = a${\mathrm{x}}^2$ + 3x − 2, biết rằng parabol có đỉnh $\mathrm{I}(-\frac{1}{2};-\frac{11}{4})$  

A. Y = ${\mathrm{x}}^2$ + 3x − 2.

B. Y = ${\mathrm{x}}^2$ + x − 4.

C. Y = 3${\mathrm{x}}^2$ + x − 1.

D. Y = 3${\mathrm{x}}^2$ + 3x − 2.