Câu hỏi:
Cho hai hàm số và . Xét các mệnh đề sau:
Đồ thị của hai hàm số f (x) và g (x) luôn cắt nhau tại một điểm.
Hàm số f(x)+g(x) đồng biến khi a > 1, nghịch biến khi 0<a<1
Đồ thị hàm số f (x) nhận trục Oy làm tiệm cận.
Chỉ có đồ thị hàm số f (x) có tiệm cận.
Hỏi có tất cả bao nhiêu mệnh đề đúng?
A. 1
B. 2
C. 3
D. 4
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem
30/11/2021 0 Lượt xem
Câu 4: Khẳng định nào dưới đây là sai khi nói về hàm số (với )
A. Trên tập xác định, hàm số đồng biến nếu a > 1, nghịch biến nếu 0 < a < 1
B. Đồ thị hàm số có một tiệm cận đứng và không có tiệm cận ngang
C. Tập xác định của hàm số là R
D. Đồ thị hàm số luôn nằm bên phải trục tung
30/11/2021 0 Lượt xem
Câu 5: Cho và các hàm . Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1)
2)
3)
4)
A. 0
B. 1
C. 2
D. 3
30/11/2021 0 Lượt xem
Câu 6: Cho a, b, c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số . Khẳng định nào sau đây là đúng?
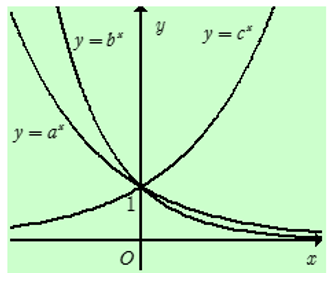

A. a>b>c
B. a<b<c
C. c>a>b
D. a>c>b
30/11/2021 0 Lượt xem

Câu hỏi trong đề: Trắc nghiệm Hàm số mũ. Hàm số Logarit có đáp án
- 0 Lượt thi
- 60 Phút
- 58 Câu hỏi
- Học sinh
Cùng danh mục Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
- 419
- 0
- 20
-
73 người đang thi
- 392
- 0
- 33
-
97 người đang thi
- 445
- 0
- 20
-
54 người đang thi
- 483
- 0
- 20
-
92 người đang thi
Chia sẻ:
Đăng Nhập để viết bình luận