Câu hỏi:
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là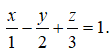 
Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
A.
B.
C. C.
D. D.
Câu 1: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;2) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. A. 2x + 2y + z - 8 = 0
B. B. 2x + 2y + z + 8 = 0
C. C.
D. D. x + 2y + 2z - 9 = 0
30/11/2021 0 Lượt xem
Câu 2: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M() và có một vectơ pháp tuyến = (-A; B; -C) là:
A. A. A(x - ) - B(y - ) + C(z - ) = 0
B. B. A(x + ) - B(y - ) + C(z + z0) = 0
C. C. A(x - ) - B(y + ) + C(z - ) = 0
D. D. A(x + ) - B(y + ) + C(z + ) = 0
30/11/2021 0 Lượt xem
Câu 3: Trong không gian Oxyz, cho điểm M(1;2;3). Lập phương trình mặt phẳng đi qua M sao cho (P) cắt các trục Ox, Oy, Oz lần lượt tại A, B, C và M là trọng tâm của tam giác ABC
A.
B. B.
C. C.
D. 3x+6y+9z=1
30/11/2021 0 Lượt xem
Câu 4: Trong không gian Oxyz, cho điểm A(2;-3;4). Lập phương trình mặt phẳng (P) đi qua các hình chiếu vuông góc của điểm A trên các trục tọa độ:
A. 2x-3y+4z-29=0
B. B. 2x-3y+4z-1=0
C.
D. D.
30/11/2021 0 Lượt xem
Câu 5: Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(-2 ;1 ;-2) và vuông góc với trục Oz.
A. A. x + y + 1 = 0
B. -2x + y - z + 1 = 0
C. C. z - 1 = 0
D. z + 2 = 0
30/11/2021 0 Lượt xem
Câu 6: Trong không gian Oxyz, lập phương trình mặt phẳng (P) đi qua điểm A(2;-1;-2) và song song với mặt phẳng (Q): 2x - y + 2z = 0
A. A. 2x - y + 2z - 1 = 0
B. B. 2x - y + 2z + 9 = 0
C. 2x - y - 2z + 1 = 0
D. 2x - y + 2z + 1 = 0
30/11/2021 0 Lượt xem
Câu hỏi trong đề: 66 câu trắc nghiệm: Phương trình mặt phẳng có đáp án (P1)
- 0 Lượt thi
- 40 Phút
- 31 Câu hỏi
- Học sinh
Cùng danh mục Chương 3: Phương pháp tọa độ trong không gian
- 273
- 0
- 25
-
40 người đang thi
- 235
- 1
- 15
-
64 người đang thi
- 251
- 2
- 15
-
53 người đang thi
- 218
- 2
- 15
-
58 người đang thi
Chia sẻ:
Đăng Nhập để viết bình luận