Câu hỏi: Cho mạng G, điểm phát s điểm thu t. Lát cắt (X, Y) được gọi là lát cắt hẹp nhất nếu:
A. khả năng thông qua của lát cắt (X,Y) bằng tổng khả năng thông qua của các cung đi ra khỏi đỉnh s
B. khả năng thông qua của lát cắt (X,Y) bằng tổng khả năng thông qua của các cung đi vào đỉnh t
C. khả năng thông qua của lát cắt (X,Y) lớn nhất.
D. khả năng thông qua của lát cắt (X,Y) bé nhất.
Câu 1: Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán BFS(I) là: 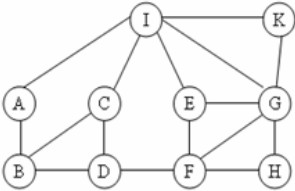
A. I, A, C, H, E, G, B, D, F, K
B. I, A, B, C, D, E, G, F, H, K
C. I, A, C, K, E, G, B, D, F, H
D. I, E, F, G, H, A, B, C, D, K
30/08/2021 0 Lượt xem
Câu 2: Mạng là một đồ thị có hướng,
A. trong đó có một đỉnh cô lập. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung e.
B. trong đó có duy nhất một đỉnh s không có cung đi vào gọi là điểm phát, có duy nhất một đỉnh t không có cung đi ra gọi là điểm thu. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung
C. trong đó có duy nhất một đỉnh s có cung đi vào gọi là điểm phát, có duy nhất một đỉnh t có cung đi ra gọi là điểm thu. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung
D. trong đó có duy nhất một đỉnh s có cung đi vào gọi là điểm phát, có duy nhất một đỉnh t không có cung đi ra gọi là điểm thu. Mỗi cung \(e = ({v_i}{\rm{ }},{v_j}){\rm{ }} \times {\rm{ }}E\) được gán một giá trị không âm qij gọi là khả năng thông qua của cung
30/08/2021 0 Lượt xem
30/08/2021 0 Lượt xem
Câu 4: Biểu thức \((P \wedge Q) \to (P \vee Q)\) tương đương logic với biểu thức nào sau đây?
A. \((P \wedge Q) \vee (P \vee Q)\)
B. \((P \wedge Q) \vee (\overline {P \vee Q} )\)
C. \((\overline {P \wedge Q} ) \vee (P \vee Q)\)
D. \((\overline {P \wedge Q} ) \wedge (P \vee Q)\)
30/08/2021 0 Lượt xem
Câu 5: Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán DFS(A) là: 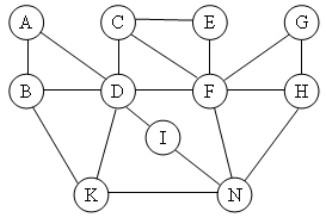
A. A, B, K, D, C, E, F, G, H, N, I
B. A, B, D, K, I, N, C, E, G, H, F
C. A, C, E, F, D, B, I, N, K, H, B
D. A, K, N, D, F, H, G, E, C, I, B
30/08/2021 0 Lượt xem
Câu 6: Cho đồ thị như hình vẽ. Kết quả khi duyệt đồ thị theo thuật toán DFS(C) là: 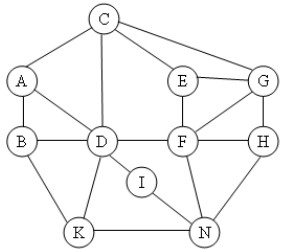
A. C, A, B, E, F, D, G, H, K, C, N
B. C, A, B, K, N, I, D, E, F, H, G
C. C, A, E, G, B, D, F, H, K, I, N
D. C, A, E, G, F, H, N, B, D, I, K
30/08/2021 0 Lượt xem

Câu hỏi trong đề: Bộ câu hỏi trắc nghiệm môn Toán rời rạc - Phần 12
- 25 Lượt thi
- 60 Phút
- 30 Câu hỏi
- Sinh viên
Cùng chủ đề Bộ câu hỏi trắc nghiệm môn Toán rời rạc có đáp án
- 2.6K
- 206
- 30
-
11 người đang thi
- 932
- 72
- 30
-
52 người đang thi
- 976
- 47
- 30
-
16 người đang thi
- 625
- 33
- 30
-
79 người đang thi




Chia sẻ:
Đăng Nhập để viết bình luận