Câu hỏi:

Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm giao tuyến của (MAB) với (SCD).

A. Giao tuyến của (MAB) với (SCD) là điểm M

B. Giao điểm của (MAB) với (SCD) là đường thẳng MN, với N là giao điểm của SD và đường thẳng đi qua M, song song với AB.

C. Giao tuyến của (MAB) với (SCD) là đường thẳng MN, với N là giao điểm của MB và SD.

D. Giao tuyến của (MAB) với (SCD) là đường thẳng MN, với N là giao điểm của MA và SD.

Câu 1:

Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, điểm N thuộc cạnh SC sao cho 2NC = NS, M là trọng tâm của tam giác CBD. Phát biểu nào sau đây là đúng?

A. MN song song với SA

B. MN và SA cắt nhau

C. MN và SA chéo nhau

D. MN và SA không đồng phẳng.

Câu 2:

Cho hai đường thẳng a và b chéo nhau. Xét hai đường thẳng p, q mà mà mỗi đường đều cắt cả a và b. Trường hợp nào sau đây không thể xảy ra.

A. p cắt q

B. p ≡ q

C. p // q

D. p và q chéo nhau

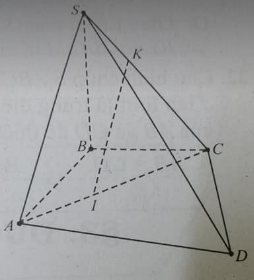
Câu 3:

Cho hình chóp S.ABCD. trên các cạnh AC, SC lấy lần lượt các điểm I, K sao cho: $\frac{SC}{SK} = \frac{AC}{AI}$

mặt phẳng (α) đi qua IK cắt các đường thẳng AB, AD, SD, SB tại các điểm theo thứ tự là M, N, P, Q. Khẳng định nào sau đây là đúng?

A. MQ và NP cắt nhau

B. tứ giác MNPQ là hình bình hành

C. tứ giác MNPQ không có cặp cạnh nào song song

D. MQ // NP

Câu 4:

Giả sử có ba đường thẳng a, b, c trong đó b // a và c //a. những phát biểu nào sau đây là sai?

(1) Nếu mặt phẳng (a, b) không trùng với mặt phẳng (a, c) thì b và c chéo nhau.

(2) Nếu mặt phẳng (a,b) trùng với mặt phẳng (a, c) thì ba đường thẳng a, b, c song song với nhau từng đôi một.

 (3) Dù cho hai mặt phẳng (a, b) và (a, c) có trùng nhau hay không, ta vẫn có b // c.

A. Chỉ có (1) sai.

B. Chỉ có (2) sai

C. Chỉ có (3) sai

D. (1), (2) và (3) đều sai

Câu 5:

Cho hai đường thẳng a và b chéo nhau. Những phát biểu nào sau đây là sai?

(1) tồn tại hai đường thẳng c, d song song với nhau, mỗi đường đều cắt cả a và b.

(2) không thể tồn tại hai đường thẳng c, d phân biệt, mỗi đường đều cắt cả a và b.

(3) không thể tồn tại một đường thẳng cắt cả a và b.

A. chỉ có (1) sai

B. chỉ có (2) sai

C. chỉ có (3) sai

D. (1), (2) và (3) đều sai.

Câu 6:

Trong các phát biểu sau, phát biểu nào đúng?

A. Hai đường thẳng không có điểm chung thì song song với nhau

B. Hai đường thẳng không có điểm chung thì chéo nhau

C. Hai đường thẳng phân biệt không cắt nhau thì song song

D. Hai đường thẳng không cùng nằm trên một mặt phẳng thì chéo nhau.