Câu hỏi:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2) và B (3; 4). Điểm P ( ; 0) (với là phân số tối giản, b > 0) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính S = a + b.
A. S = -2
B. S = 8
C. S = 7
D. S = 4
Câu 1: Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; h là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
A. y = 4,9 + 12,2t + 1,2.
B. y = −4,9 + 12,2t + 1,2.
C. y = −4,9 + 12,2t − 1,2.
D. y = −4,9 − 12,2t + 1,2.
30/11/2021 0 Lượt xem
Câu 2: Tìm m để hàm số y = − 2x + 2m + 3 có giá trị nhỏ nhất trên đoạn [2; 5] bằng −3.
A. m = -3
B. m = -9
C. m = 1
D. m = 0
30/11/2021 0 Lượt xem
Câu 3: Cho parabol (P): y = a + bx + c (a 0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax2 + bx + c| = m có bốn nghiệm phân biệt.
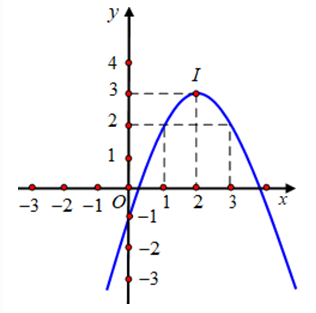

A. −1 < m < 3
B. 0 < m < 3.
C. 0 m 3.
D. −1 m 3.
30/11/2021 0 Lượt xem
Câu 4: Tìm tất cả các giá trị mm để đường thẳng y = mx + 3 − 2m cắt parabol y = − 3x − 5 tại 2 điểm phân biệt có hoành độ trái dấu.
A. m < −3
B. −3 < m < 4
C. m < 4
D. m 4
30/11/2021 0 Lượt xem
Câu 5: Đồ thị hàm số y = x − 2m + 1 tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng . Khi đó m bằng:
A. m = 2; m = 3.
B. m = 2; m = 4.
C. m = −2; m = 3.
D. m = −2.
30/11/2021 0 Lượt xem
Câu 6: Hỏi có bao nhiêu giá trị mm nguyên trong nửa khoảng (0; 2017] để phương trình | − 4|x |−5| − m = 0 có hai nghiệm phân biệt?
A. 2016
B. 2008
C. 2009
D. 2017
30/11/2021 0 Lượt xem

- 0 Lượt thi
- 50 Phút
- 12 Câu hỏi
- Học sinh
Cùng danh mục Trắc nghiệm tổng hợp Toán 10
- 596
- 0
- 50
-
20 người đang thi
- 413
- 1
- 14
-
98 người đang thi
Chia sẻ:
Đăng Nhập để viết bình luận