Câu hỏi:

Trong không gian Oxyz, cho hai điểm A(1;0;-2), B(-1;1;1). Phương trình mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:

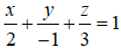
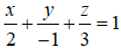
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;1 ;-3), vuông góc với mặt phẳng (Q): x + y - 3z = 0 đồng thời (P) song song với trục Oz.

Trong không gian Oxyz, cho ba điểm thay đổi A(a; 0; 0), B(0; b; 0), C(0; 0; c) trong đó a, b, c khác 0 và thỏa mãn điều kiện 3ab + bc - 2ac = abc . Khoảng cách lớn nhất từ O đến mặt phẳng (ABC) là:

Trong không gian Oxyz, cho điểm M(-x₀; -y₀; z₀) và phương trình của mặt phẳng (P): Ax + By + Cz + D = 0. Khoảng cách từ điểm M đến mặt phẳng (P) là:

Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(${\mathrm{x}}_0, {\mathrm{y}}_0, {\mathrm{z}}_0$) và có một vectơ pháp tuyến $\overrightarrow{{\mathrm{n}}_{\mathrm{P}}}$ = (A; B; C) là:

Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(3;2;1) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho tam giác ABC đều. Số mặt phẳng (P) thỏa mãn bài toán là:

Trong không gian Oxyz, phương trình tổng quát của mặt phẳng (P) đi qua điểm M(1;-2;3) và song song với mặt phẳng (Oxy) là: