Câu hỏi:

Cho phương trình \(\frac{1}{4}{x^2} - \left( {m - 3} \right)x + {m^2} - 2m + 7 = 0\).Tìm m để phương trình có hai nghiệm phân biệt.

A. \(m \ge \frac{1}{2}\)

B. \(m < - \frac{1}{2}\)

C. \(m > \frac{1}{2}\)

D. \(m < \frac{1}{2}\)

Câu 1:

Cho tam giác ABC có H là trực tâm. Biểu thức \({\left( {\overrightarrow {AB} + \overrightarrow {HC} } \right)^2}\) bằng biểu thức nào sau đây?

A. \(A{B^2} + H{C^2}\)

B. \({\left( {AB + HC} \right)^2}\)

C. \(A{C^2} + A{H^2}\)

D. \(A{C^2} + 2A{H^2}.\)

Câu 2:

Tìm tất cả các giá trị của m để phương trình \({m^2}\left( {x + m} \right) = x + m\) có vô số nghiệm?

A. \(m = \pm1\)

B. m = 0 hoặc m = 1

C. m = 0 hoặc m = -1

D. \( - 1 < m < 1,\,m \ne 0\)

Câu 3:

Biết \(\cos \alpha = \frac{1}{3}\). Giá trị đúng của biểu thức \(P = {\sin ^2}\alpha + 3{\cos ^2}\alpha \) bằng bao nhiêu?

A. \(\dfrac13\)

B. \(\dfrac{{10}}{9}\)

C. \(\dfrac{{11}}{9}\)

D. \(\dfrac{{4}}{3}\)

Câu 4:

Cho parabol \(\left( P \right):y = a{x^2} + bx + c\) có đồ thị như hình bên. Phương trình của parabol này là phương trình nào dưới đây?

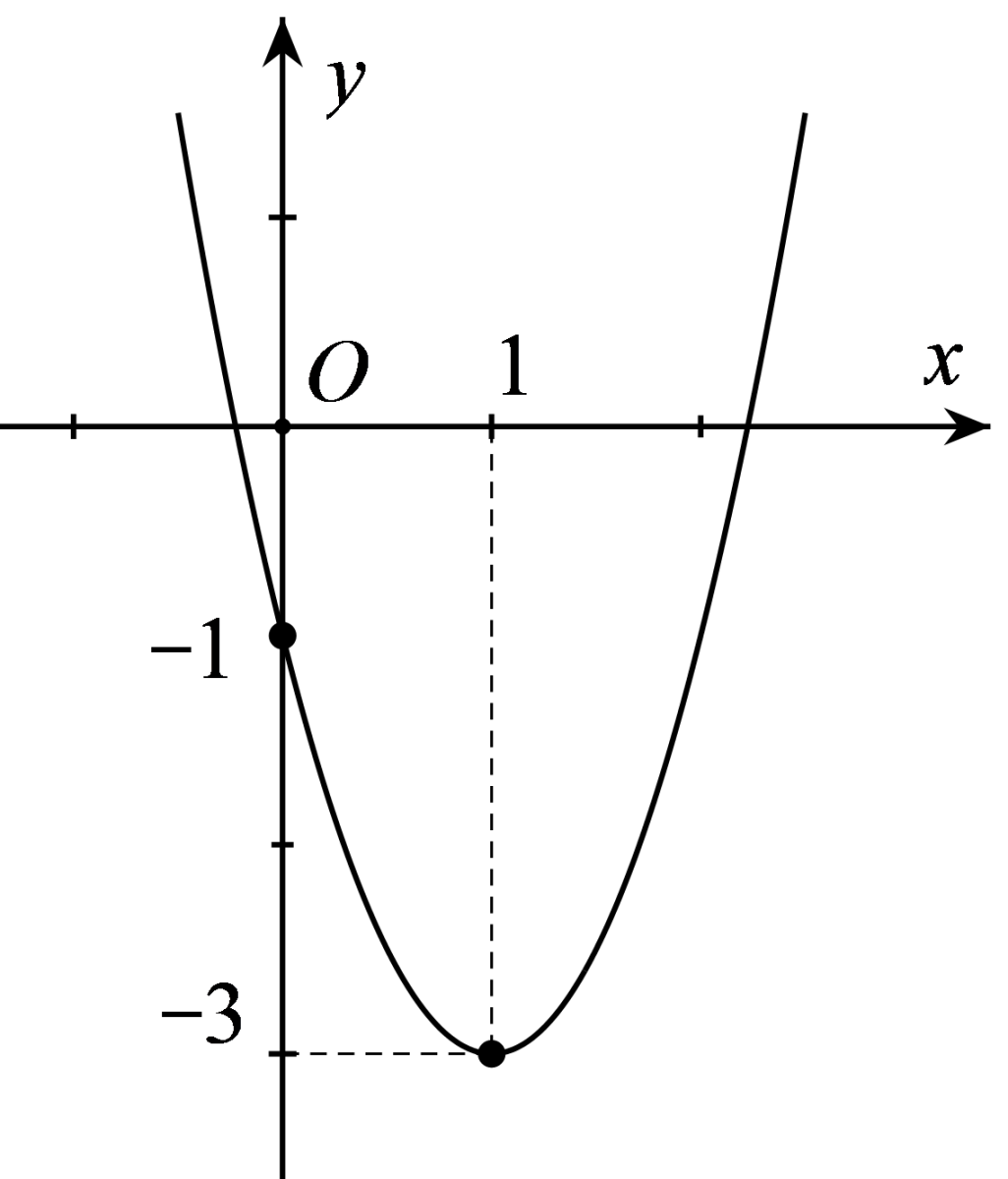
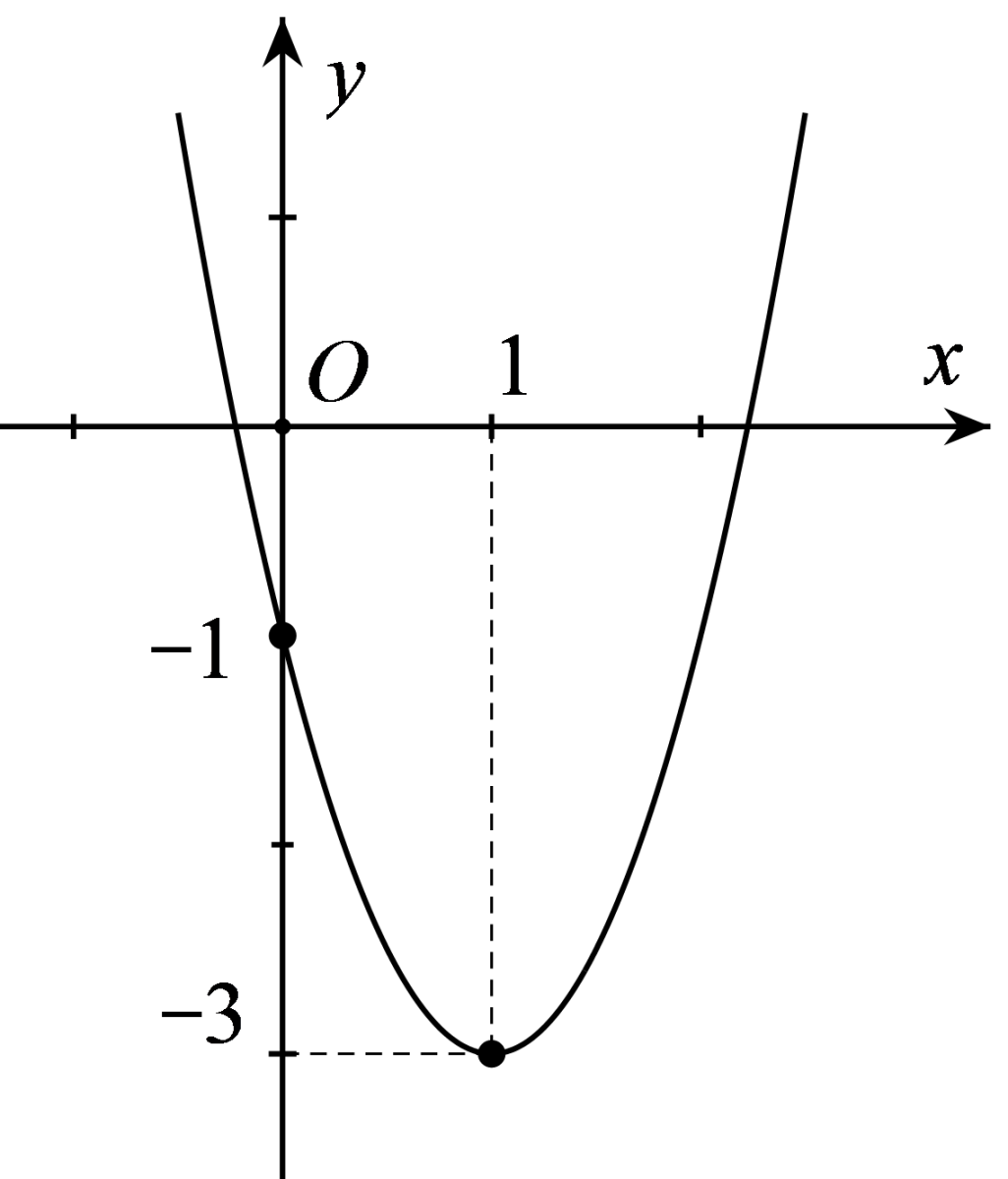
A. \(y = 2{x^2} - 4x - 1\)

B. \(y = 2{x^2} + 3x - 1\)

C. \(y = 2{x^2} + 8x - 1\)

D. \(y = 2{x^2} - x - 1\)

Câu 5:

Cho hình chữ nhật ABCD có \(AB = \sqrt 2 ,\) AD = 1. Tính góc giữa hai vec tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} .\)

A. 89o

B. 92o

C. 109o

D. 91o

Câu 6:

Tìm giao điểm của parabol \(y = {x^2} - 3{\rm{x}} + 2\) với đường thẳng \(y = x - 1\).

A. \(\left( {1;0} \right),{\rm{ }}\left( {3;2} \right).\)

B. \(\left( {0; - 1} \right),\left( { - 2; - 3} \right).\)

C. (-1; 2); (2;1)

D. (2; 1); (0; -1)