Câu hỏi:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
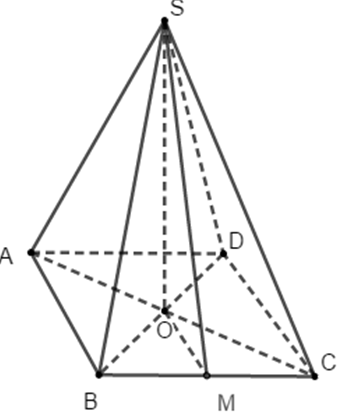
Tan của góc giữa mặt bên và mặt đáy bằng:
A.
30/11/2021 0 Lượt xem
Câu 2: Cho hình lập phương ABCD.A’B’C’D’: Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
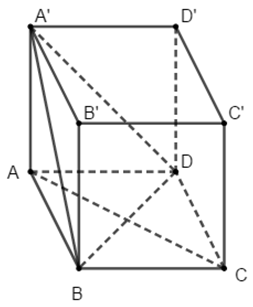

A. trung điểm của BD
B. trung điểm của A’B
C. trung điểm của A’D
D. tâm của tam giác BDA’
30/11/2021 0 Lượt xem
Câu 3: Cho hình lập phương ABCD.A’B’C’D’:
Mặt phẳng (ACC’A’) Không vuông góc với.
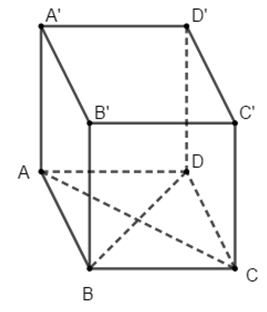

A. (ABCD)
B. (CDD’C’)
C. (BDC’)
D. (A’BD)
30/11/2021 0 Lượt xem
Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng:
A. (SAD)
B. (SBD)
C. (SDC)
D. (SBC)
30/11/2021 0 Lượt xem
Câu 5: Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Điểm cách đều bốn điểm A, B, C, D là:
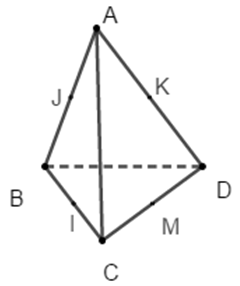

A. trung điểm J của AB
B. trung điểm I của BC
C. trung điểm K của AD
D. trung điểm M của CD
30/11/2021 0 Lượt xem
Câu 6: Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAC) và (AHK) vuông góc vì:
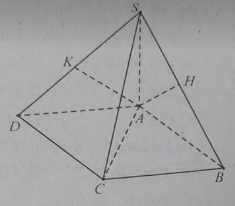

A. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD)
B. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC); và AK ⊥ (SCD) (do AK⊥SD và AK⊥CD) nên SC⊥(AHK)
C. AH ⊥(SBC) (do AH ⊥ SB và AH ⊥ BC) nên SC⊥(AHK)
D. AK ⊥(SBC) (do AK ⊥ SD và AK ⊥ CD) nên SC ⊥ (AHK)
30/11/2021 0 Lượt xem

Câu hỏi trong đề: Trắc nghiệm Mặt phẳng vuông góc có đáp án
- 0 Lượt thi
- 40 Phút
- 14 Câu hỏi
- Học sinh
Cùng danh mục Chương 3: Vectơ trong không gian. Quan hệ vuông góc trong không gian
- 343
- 0
- 22
-
24 người đang thi
- 370
- 1
- 10
-
51 người đang thi
- 347
- 0
- 15
-
95 người đang thi
- 401
- 0
- 15
-
57 người đang thi
Chia sẻ:
Đăng Nhập để viết bình luận